朝花夕拾

感知机是一种二元线性分类器，最初由Frank Rosenblatt在1957年提出。它是一种基本的神经网络模型，也是深度学习的起源之一。
感知机的工作原理是将输入向量与一组权重向量进行内积运算，然后将结果通过一个阈值函数（如阶跃函数）进行判断分类。这个阈值函数将内积的结果映射到一个二元输出（1或0），表示输入向量所属的类别。感知机的训练过程就是通过不断调整权重向量，使得分类器能够正确地分类所有的训练样本。
感知机的优点是简单、易于实现，可以处理大规模数据集，并且具有在线学习的能力，即可以在不断接收新的训练样本的情况下更新模型。缺点是只能解决线性可分问题，对于非线性问题无法处理，因此通常需要结合其他方法或模型来解决复杂问题。

如下图所示，输入向量$\vec{x}=(x1,x2)$，权重向量$\vec{w}=(w1,w2)$，输出向量$\vec{y}$

基于感知机的定义，上图的分类函数如下：

其中权重向量$\vec{w}$表达输入信号的重要程度，权重越大，说明权重所对应的信号在分类函数中的占比越大

逻辑电位

与门(AND Gate)

与门，在给定的分类函数中，当且仅当所有信号都达标时，整个分类函数的结果就是1，否则函数结果是0。与门的真值表如下：

假定信号向量$\vec{x}$元素的取值范围在集合$[0,1]$中，那么只需要找到一组$w1,w2,\theta$满足上述真值表即可。当然，满足条件的集合有无群多个，我们随便选取一个，如{0.5, 0.5, 0.7}来实现一个与门感知机

def AND(x1, x2):
    w1, w2, theta = 0.5, 0.5, 0.7
    tmp = x1 * w1 + x2 * w2
    if tmp > theta:
        return 1
    elif tmp <= theta:
        return 0
    
print(AND(0, 0), AND(1, 0), AND(0, 1), AND(1, 1))

0 0 0 1

或门(OR Gate)

或门，在给定的分类函数中，只要任意一个或者多个信号达标时，函数结果是1，否则是0。或门真值表如下：

同样，我们选一组集合{0.5, 0.5, 0.3}实现一个或门感知机

def OR(x1, x2):
    w1, w2, theta = 0.5, 0.5, 0.3
    tmp = x1 * w1 + x2 * w2
    if tmp > theta:
        return 1
    elif tmp <= theta:
        return 0
    
print(OR(0, 0), OR(1, 0), OR(0, 1), OR(1, 1))

0 1 1 1

与非门(NAND Gate)

与非门是与门取非

我们选一组集合{-0.5, -0.5, 0.7}实现一个或门感知机

def NAND(x1, x2):
    w1, w2, theta = -0.5, -0.5, -0.7
    tmp = x1 * w1 + x2 * w2
    if tmp > theta:
        return 1
    elif tmp <= theta:
        return 0
    
print(NAND(0, 0), NAND(1, 0), NAND(0, 1), NAND(1, 1))

1 1 1 0

权重和偏置

对感知器分类函数做如下转换：$b=-\theta$，那么新的分类函数如下：

其中向量$\vec{w}$即为权重，表示对应信号量的权重；b为偏置，表示神经元(分类函数)被激活(输出1)的难易程度

感知机的局限性

异或门(XOR Gate)

异或门，当且仅当两个信号不同时，函数结果是1，否则是0。异或门真值表如下：

我们发现，很难用感知机来实现异或门，因为感知机只能实现线性可分问题，而异或门是线性不可分的。如下图所示，感知机无法将两类数据分开，因为它们不是线性可分的。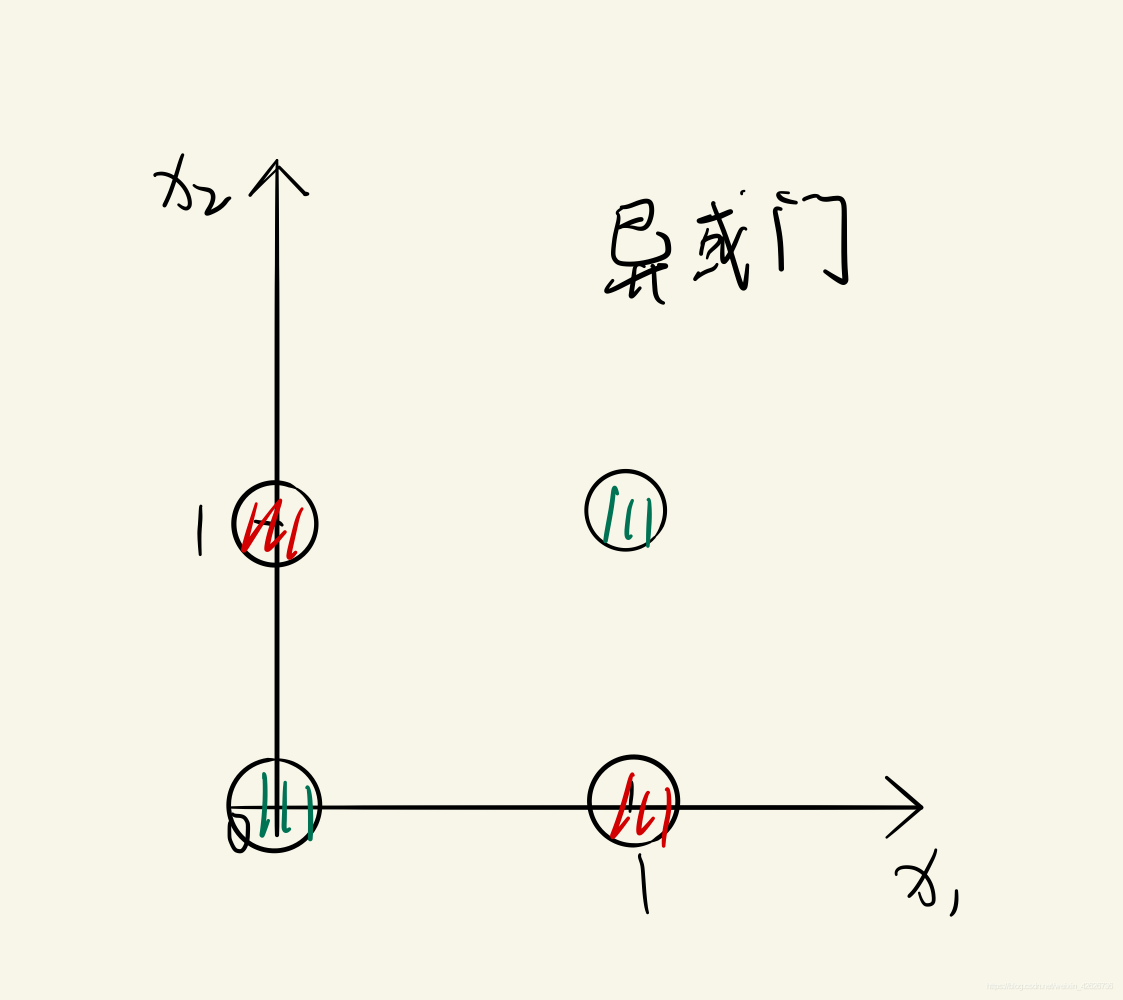

要对异或门进行分类，需要引入非线性函数，如下图所示，我们将感知机的输出作为非线性函数的输入，这样就可以实现异或门的分类了。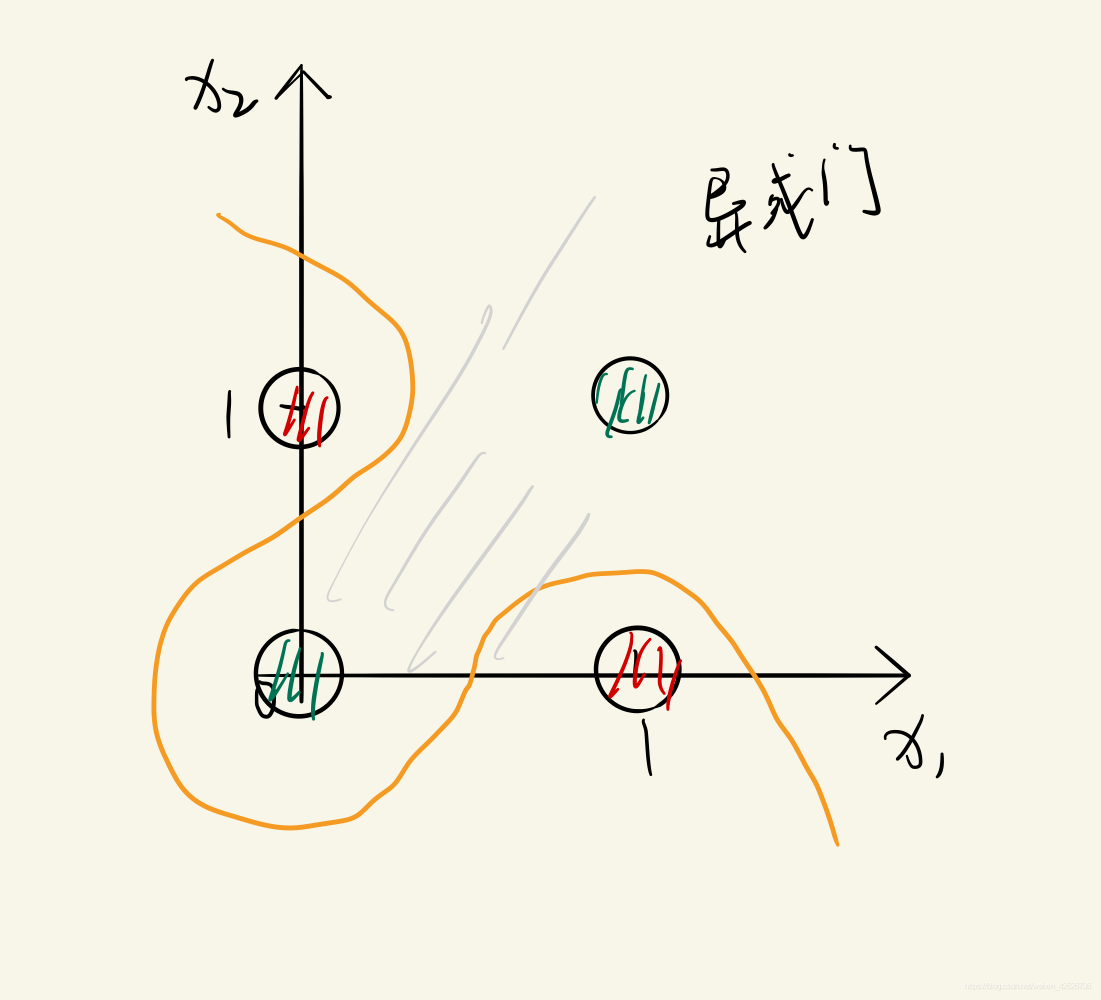

多层感知机

多层感知机，是指在感知机的基础上，增加一层或多层非线性函数，如下图所示，我们将感知机的输出作为非线性函数的输入，这样就可以实现异或门的分类了。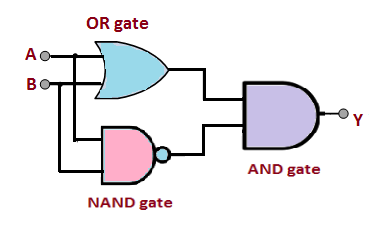

通过多层感知机实现异或门

def XOR(x1, x2):
    s1 = OR(x1, x2)
    s2 = NAND(x1, x2)
    return AND(s1, s2)

print(XOR(0, 0), XOR(1, 0), XOR(0, 1), XOR(1, 1))

0 1 1 0

异或门是一个多层感知机，它是由与门、或门、与非门组合而成的。这里我们使用了与门、或门、与非门三个门电路，如下图所示。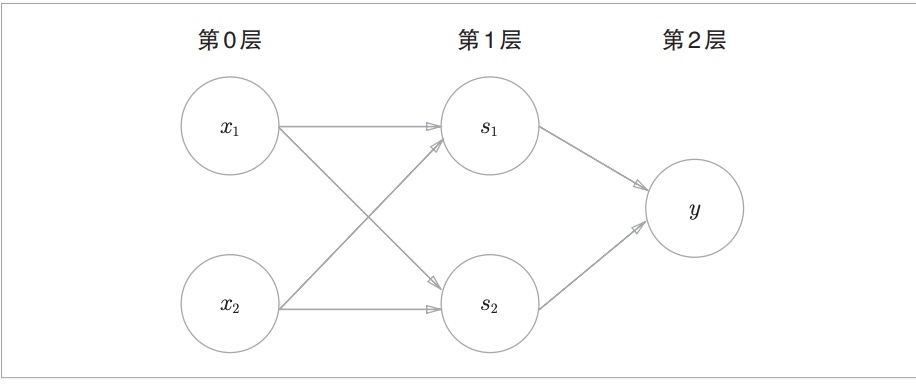

第0层有两个神经元接收输入信号，第一层接收第0层的输出信号作为输入信号进行计算，并输出最终结果y