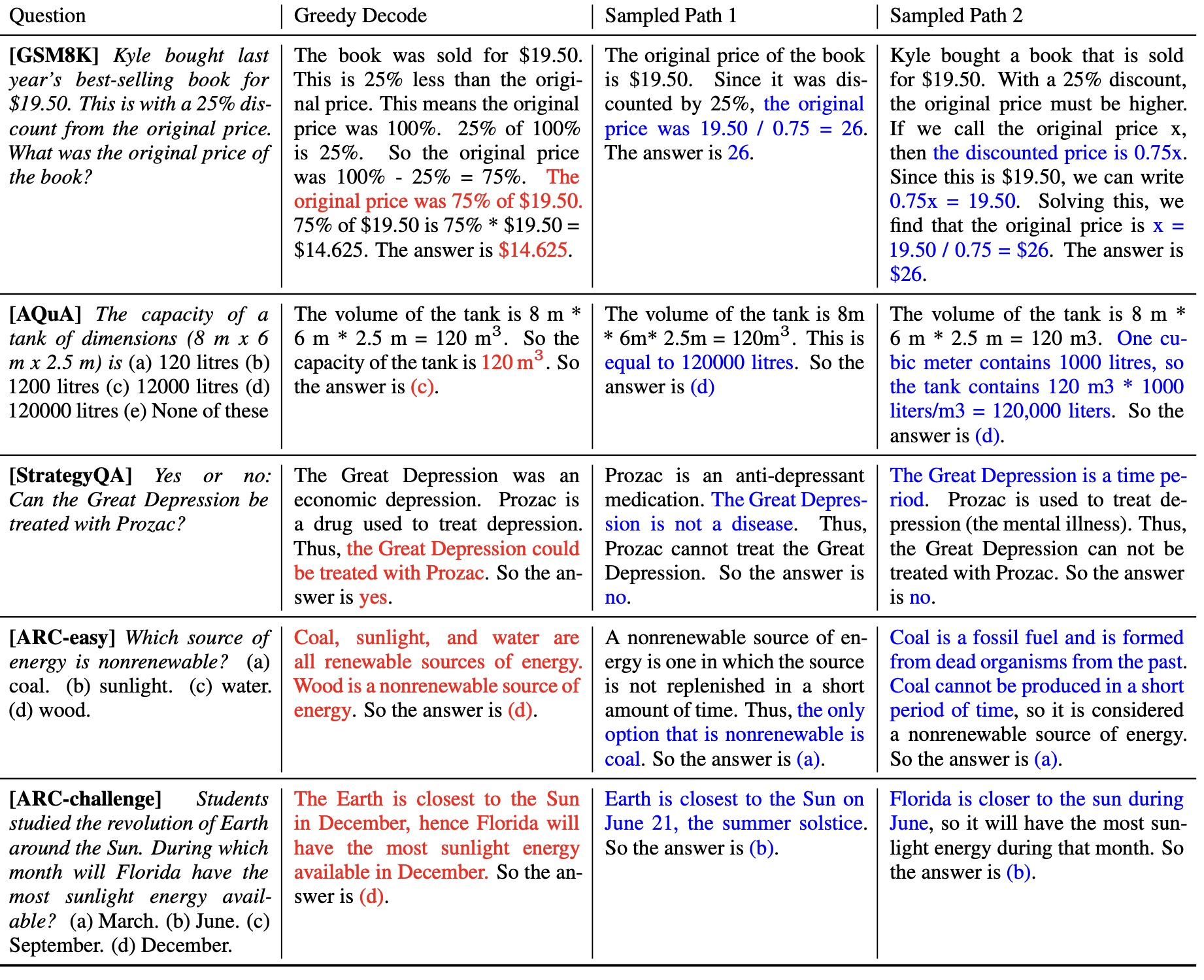
INTRODUCTION
Although language models have demonstrated remarkable success across a range of NLP tasks, their ability to demonstrate reasoning is often seen as a limitation, which cannot be overcome solely by increasing model scale (Rae et al., 2021; BIG-bench collaboration, 2021, inter alia). In an effort to address this shortcoming, Wei et al. (2022) have proposed chain-of-thought prompting, where a language model is prompted to generate a series of short sentences that mimic the reasoning process a person might employ in solving a task. For example, given the question “If there are 3 cars in the parking lot and 2 more cars arrive, how many cars are in the parking lot?”, instead of directly responding with “5”, a language model would be prompted to respond with the entire chain-of-thought: “There are 3 cars in the parking lot already. 2 more arrive. Now there are 3 + 2 = 5 cars. The answer is 5.”. It has been observed that chain-of-thought prompting significantly improves model performance across a variety of multi-step reasoning tasks (Wei et al., 2022).
In this paper, we introduce a novel decoding strategy called self-consistency to replace the greedy decoding strategy used in chain-of-thought prompting (Wei et al., 2022), that further improves language models’ reasoning performance by a significant margin. Self-consistency leverages the intuition that complex reasoning tasks typically admit multiple reasoning paths that reach a correct answer (Stanovich & West, 2000). The more that deliberate thinking and analysis is required for a problem (Evans, 2010), the greater the diversity of reasoning paths that can recover the answer.
尽管语言模型在各种自然语言处理任务中表现出了显著的成功,但它们展示推理能力的能力通常被视为一种限制,仅通过增加模型规模无法克服(Rae等人,2021;BIG-bench合作组织,2021)。为了解决这个缺点,魏等人(2022)提出了思维链提示方法,在该方法中,语言模型被提示生成一系列短句子来模仿一个人在解决任务时可能采用的推理过程。例如,在给定问题“停车场里有3辆汽车和2辆更多的汽车到达后停车场里有多少辆汽车?”时,语言模型不会直接回答“5”,而是被提示回答整个思维链:“停车场已经有3辆汽车。再来2辆。现在有3 + 2 = 5 辆汽车。答案是5。”观察发现思维链提示显著提高了各种多步推理任务上的模型性能(魏等人,2022)。
本文介绍了一种称为自我一致性的新颖解码策略来替换思维链提示中使用的贪婪解码策略(魏等人,2022),进一步大幅提高了语言模型的推理性能。自我一致性利用了复杂推理任务通常允许多个推理路径达到正确答案的直觉(Stanovich&West,2000)。对于需要深思熟虑和分析的问题(Evans,2010),恰当的思考和分析越多,则可以恢复答案的不同推理路径就越多。
Figure 1 illustrates the self-consistency method with an example. We first prompt the language model with chain-of-thought prompting, then instead of greedily decoding the optimal reasoning path, we propose a “sample-and-marginalize” decoding procedure: we first sample from the language model’s decoder to generate a diverse set of reasoning paths; each reasoning path might lead to a different final answer, so we determine the optimal answer by marginalizing out the sampled reasoning paths to find the most consistent answer in the final answer set. Such an approach is analogous to the human experience that if multiple different ways of thinking lead to the same answer, one has greater confidence that the final answer is correct. Compared to other decoding methods, self-consistency avoids the repetitiveness and local-optimality that plague greedy decoding, while mitigating the stochasticity of a single sampled generation
图1展示了自洽方法的一个例子。我们首先使用思维链提示来激活语言模型,然后不是贪心地解码最优推理路径,而是提出了一种“采样和边缘化”解码过程:我们首先从语言模型的解码器中进行采样以生成多样化的推理路径;每个推理路径可能导致不同的最终答案,因此我们通过边缘化采样到的推理路径来确定最佳答案,并在最终答案集合中找到最一致的答案。这种方法类似于人类经验:如果多种不同方式的思考都导致相同的答案,则可以更有信心地认为该答案是正确的。与其他解码方法相比,自洽避免了贪婪解码所困扰的重复性和局部优化问题,同时减轻了单次采样生成带来的随机性。
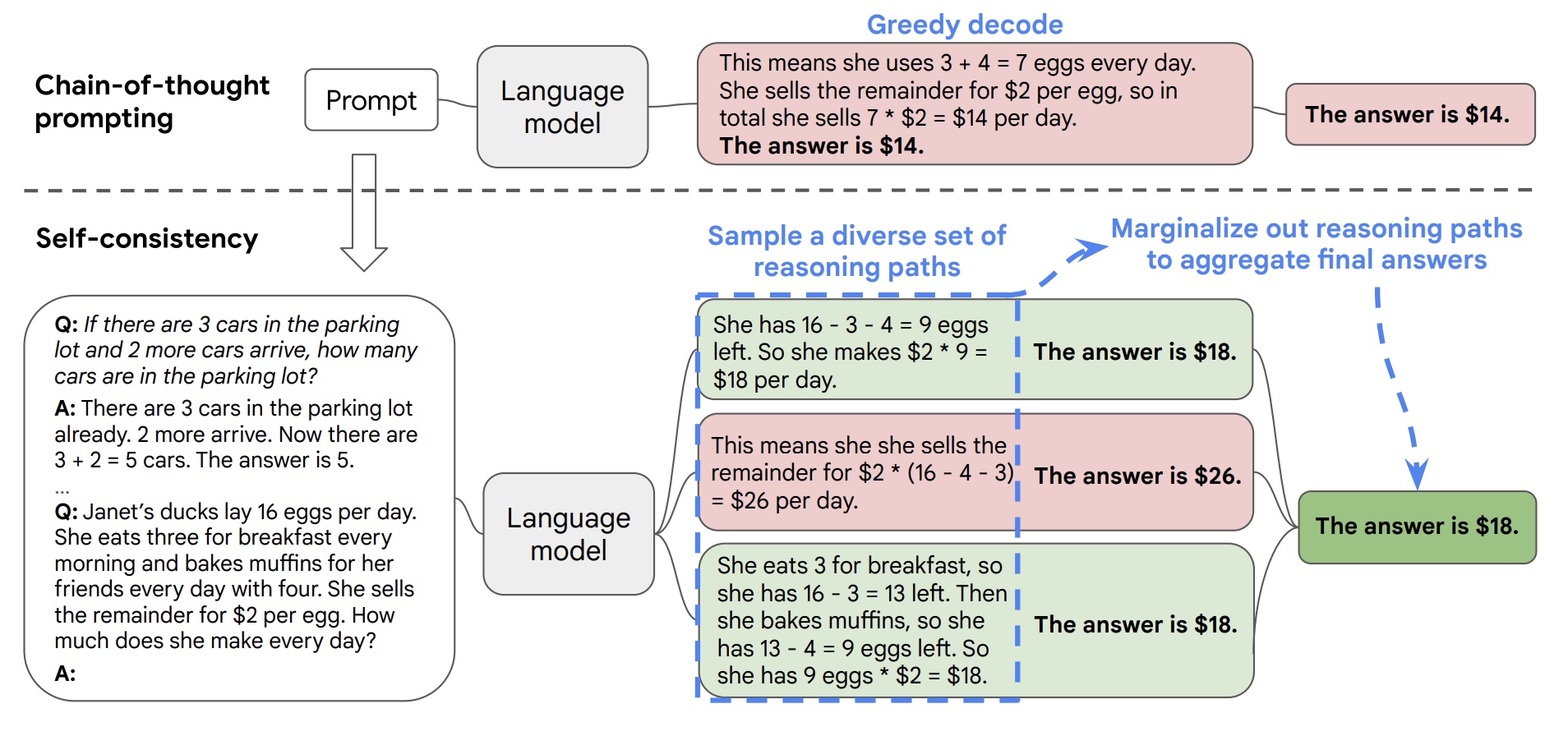
Figure 1: The self-consistency method contains three steps: (1) prompt a language model using chain-of-thought (CoT) prompting; (2) replace the “greedy decode” in CoT prompting by sampling from the language model’s decoder to generate a diverse set of reasoning paths; and (3) marginalize out the reasoning paths and aggregate by choosing the most consistent answer in the final answer set.
图1:自一致性方法包含三个步骤:(1)使用思维链(CoT)提示来提示语言模型;(2)将CoT提示中的“贪婪解码”替换为从语言模型的解码器中采样,以生成多样化的推理路径;并且(3)通过选择最一致的答案集合中最一致的答案来边缘化推理路径并聚合。
Self-consistency is far simpler than prior approaches that either train an additional verifier (Cobbe et al., 2021) or train a re-ranker given additional human annotations to improve generation quality (Thoppilan et al., 2022). Instead, self-consistency is entirely unsupervised, works off-the-shelf with pre-trained language models, requires no additional human annotation, and avoids any additional training, auxiliary models or fine-tuning. Self-consistency also differs from a typical ensemble approach where multiple models are trained and the outputs from each model are aggregated, it acts more like a “self-ensemble” that works on top of a single language model.
自我一致性比之前的方法要简单得多,之前的方法要么训练一个额外的验证器(Cobbe等人,2021),要么在给定额外人工注释以提高生成质量时训练一个重新排序模型(Thoppilan等人,2022)。相反,自我一致性完全是无监督的,在预先训练好的语言模型上即可使用,并且不需要任何额外的人工注释、避免了任何附加培训、辅助模型或微调。自我一致性还与典型集成方法有所不同,典型集成方法会训练多个模型并聚合每个模型的输出结果,而它更像是一个“自我集成”,可以在单个语言模型上运行。
We evaluate self-consistency on a wide range of arithmetic and commonsense reasoning tasks over
four language models with varying scales: the public UL2-20B (Tay et al., 2022) and GPT-3-175B
(Brown et al., 2020), and two densely-activated decoder-only language models: LaMDA-137B
(Thoppilan et al., 2022) and PaLM-540B (Chowdhery et al., 2022). On all four language models,
self-consistency improves over chain-of-thought prompting by a striking margin across all tasks. In
particular, when used with PaLM-540B or GPT-3, self-consistency achieves new state-of-the-art levels
of performance across arithmetic reasoning tasks, including GSM8K (Cobbe et al., 2021) (+17.9%
absolute accuracy gains), SVAMP (Patel et al., 2021) (+11.0%), AQuA (Ling et al., 2017) (+12.2%),
and across commonsense reasoning tasks such as StrategyQA (Geva et al., 2021) (+6.4%) and ARCchallenge (Clark et al., 2018) (+3.9%). In additional experiments, we show self-consistency can
robustly boost performance on NLP tasks where adding a chain-of-thought might hurt performance
compared to standard prompting (Ye & Durrett, 2022). We also show self-consistency significantly
outperforms sample-and-rank, beam search, ensemble-based approaches, and is robust to sampling
strategies and imperfect prompts.
我们在广泛的算术和常识推理任务上评估了四个语言模型的自一致性,这些模型具有不同的规模:公共UL2-20B(Tay等人,2022)和GPT-3-175B(Brown等人,2020),以及两个密集激活的仅解码器语言模型:LaMDA-137B(Thoppilan等人,2022)和PaLM-540B(Chowdhery等人,2022)。在所有四个语言模型中,自一致性相对于思维链提示显著提高了所有任务的表现。特别是,在与PaLM-540B或GPT-3配合使用时,在算术推理任务中实现了新的最先进水平,并取得了巨大成功。包括GSM8K(Cobbe等人,2021)(+17.9%绝对准确率增益),SVAMP (Patel et al., 2021) (+11.0%)、AQuA (Ling et al., 2017) (+12.2%)以及常识推理任务如StrategyQA(Geva et al., 2021)(+6.4%) 和ARCchallenge(Clark et al., 2018)(+3.9%). 在额外实验中, 我们展示出自一致性可以稳健地提升NLP任务表现, 而添加思维链可能会降低表现( Ye & Durrett, 2022)。我们还展示了自一致性明显优于样本排序、波束搜索、基于集成的方法,并且对采样策略和不完美提示具有鲁棒性。
SELF-CONSISTENCY OVER DIVERSE REASONING PATHS
A salient aspect of humanity is that people think differently. It is natural to suppose that in tasks
requiring deliberate thinking, there are likely several ways to attack the problem. We propose that
such a process can be simulated in language models via sampling from the language model’s decoder.
For instance, as shown in Figure 1, a model can generate several plausible responses to a math
question that all arrive at the same correct answer (Outputs 1 and 3). Since language models are not
perfect reasoners, the model might also produce an incorrect reasoning path or make a mistake in
one of the reasoning steps (e.g., in Output 2), but such solutions are less likely to arrive at the same
answer. That is, we hypothesize that correct reasoning processes, even if they are diverse, tend to
have greater agreement in their final answer than incorrect processes.
人类的一个显著特点是人们思考方式不同。在需要深思熟虑的任务中,有多种方法可以解决问题是很自然的想法。我们提出这样一个过程可以通过从语言模型解码器中进行抽样来模拟。例如,如图1所示,模型可以生成几个合理的答案来回答数学问题(输出1和3)。由于语言模型并非完美推理者,因此该模型可能还会产生错误的推理路径或在某些推理步骤上出错(例如,在输出2中),但这样的解决方案不太可能得到相同的答案。也就是说,我们假设正确的推理过程即使它们是多样化的,在最终答案上正确答案比错误答案能容易达成一致。
We leverage this intuition by proposing the following self-consistency method. First, a language
model is prompted with a set of manually written chain-of-thought exemplars (Wei et al., 2022). Next,
we sample a set of candidate outputs from the language model’s decoder, generating a diverse set of
candidate reasoning paths. Self-consistency is compatible with most existing sampling algorithms,
including temperature sampling (Ackley et al., 1985; Ficler & Goldberg, 2017), top-k sampling (Fan
et al., 2018; Holtzman et al., 2018; Radford et al., 2019), and nucleus sampling (Holtzman et al.,
2020). Finally, we aggregate the answers by marginalizing out the sampled reasoning paths and
choosing the answer that is the most consistent among the generated answers.
我们通过提出以下自一致性方法来利用这种直觉。首先,语言模型会提示一组手动编写的思维链示例(Wei等人,2022)。接下来,我们从语言模型的解码器中采样一组候选输出,生成多样化的候选推理路径。自一致性与大多数现有的采样算法兼容,包括温度采样(Ackley等人,1985;Ficler和Goldberg,2017)、前k个最高概率值采样(Fan等人,2018;Holtzman等人,2018;Radford等人,2019)和核心区域采样(Holtzman等人,2020)。最后,在边缘化所取得的推理路径答案之后聚合答案,并选择在生成答案中最为一致的答案。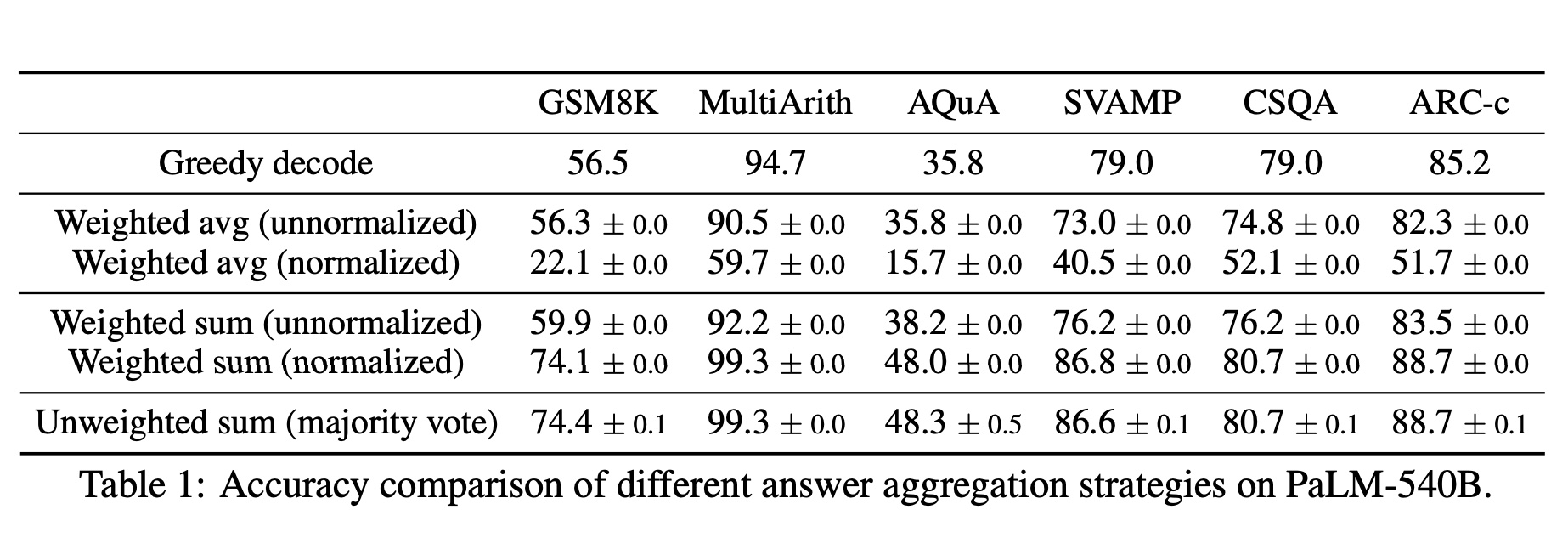
In more detail, assume the generated answers ai are from a fixed answer set, ai ∈ A, wherei = 1, . . . , m indexes the m candidate outputs sampled from the decoder. Given a prompt and a question, self-consistency introduces an additional latent variable ri
, which is a sequence of tokens representing the reasoning path in the i-th output, then couples the generation of (ri, ai) where ri → ai, i.e., generating a reasoning path ri is optional and only used to reach the final answer ai. As an example, consider Output 3 from Figure 1: the first few sentences “She eats 3 for breakfast … So she has 9 eggs * $2 = $18.” constitutes ri, while the answer 18 from the last sentence, “The answer is $18”, is parsed as ai.1 After sampling multiple (ri, ai) from the model’s decoder, self-consistency applies a marginalization over ri by taking a majority vote over ai, i.e., arg
, or as we defined as the most “consistent” answer among the final answer set.
更详细地说,假设生成的答案ai来自一个固定的答案集合A,其中i = 1, . . . , m索引从解码器中抽样的m个候选输出。给定提示和问题,自一致性引入了另一个潜在变量ri,它是表示第i个输出中推理路径的令牌序列,然后将(ri, ai) 的生成耦合起来,其中 ri → ai ,即生成推理路径ri是可选的,并且仅用于达到最终答案ai。例如,请考虑图1中的Output 3:前几句话“She eats 3 for breakfast … So she has 9 eggs * $2 = $18.”构成了ri,而最后一句话“ The answer is $18” 中的答案18被解析为ai。在从模型解码器中抽取多个(ri, ai)之后,自一致性通过对ai进行大多数投票来对ri进行边缘化处理,即arg maxa Pm i=1 1(ai=a),或者我们定义为最终答案集合中最“一致”的答案。
In Table 1, we show the test accuracy over a set of reasoning tasks by using different answer
aggregation strategies. In addition to majority vote, one can also weight each (ri, ai) by P(ri, ai|prompt, question) when aggregating the answers. Note to compute P(ri, ai| prompt, question), wecan either take the unnormalized probability of the model generating (ri, ai) given (prompt, question),or we can normalize the conditional probability by the output length (Brown et al., 2020), i.e.,
在表1中,我们展示了使用不同答案聚合策略在一组推理任务上的测试准确性。除了多数投票外,在聚合答案时还可以通过P(ri, ai|prompt, question)对每个(ri, ai)进行加权。请注意,为计算P(ri, ai| prompt, question),我们可以采用模型生成(ri,ai)给定(prompt,question)的未归一化概率或将条件概率通过输出长度进行归一化(Brown等人,2020)。
where log P(tk | prompt, question, t1, . . . , tk−1) is the log probability of generating the k-th token tk in (ri, ai) conditioned on the previous tokens, and K is the total number of tokens in (ri, ai).In Table 1, we show that taking the “unweighted sum”, i.e., taking a majority vote directly over ai yields a very similar accuracy as aggregating using the “normalized weighted sum”. We took a closer look at the model’s output probabilities and found this is because for each (ri, ai), the normalized conditional probabilities P(ri, ai| prompt, question) are quite close to each other, i.e., the language model regards those generations as “similarly likely”.2 Additionally, when aggregating the answers,the results in Table 1 show that the “normalized” weighted sum (i.e., Equation 1) yields a much higher accuracy compared to its unnormalized counterpart. For completeness, in Table 1 we also report the results by taking a “weighted average”, i.e., each a gets a score of its weighted sum divided by , which results in a much worse performance.
在这里,log P(tk | prompt, question, t1, . . . , tk−1) 是在前面的标记条件下生成第k个标记tk的对数概率,在(ri,ai)中的总标记数为K。在表格1中,我们展示了采用“未加权求和”的方法即直接对ai进行多数投票与使用“归一化加权求和”进行聚合所得到的准确性非常相似。我们仔细观察了模型输出概率,并发现这是因为对于每个(ri,ai),规范化条件概率P(ri, ai| prompt, question)非常接近,即语言模型认为那些生成结果是“同等可能”的。此外,在聚合答案时,在表格1中显示,“归一化”加权求和(即方程式1)相比其未归一化版本具有更高的准确性。为了完整起见,在表格1中我们还报告了通过采用“加权平均值”的方法来计算结果,即每个a都获得其加权总和除以 的分数,并且该方法导致性能大幅下降。
Self-consistency explores an interesting space between open-ended text generation and optimal text generation with a fixed answer. Reasoning tasks typically have fixed answers, which is why researchers have generally considered greedy decoding approaches (Radford et al., 2019; Wei et al.,2022; Chowdhery et al., 2022). However, we have found that even when the desired answer is fixed,introducing diversity in the reasoning processes can be highly beneficial; therefore we leverage sampling, as commonly used for open-ended text generation (Radford et al., 2019; Brown et al., 2020;Thoppilan et al., 2022), to achieve this goal. One should note that self-consistency can be applied only to problems where the final answer is from a fixed answer set, but in principle this approach can be extended to open-text generation problems if a good metric of consistency can be defined between multiple generations, e.g., whether two answers agree or contradict each other.
自一致性探索了开放式文本生成和具有固定答案的最优文本生成之间的一个有趣空间。推理任务通常具有固定答案,这就是为什么研究人员通常考虑贪婪解码方法(Radford等人,2019;Wei等人,2022;Chowdhery等人,2022)的原因。然而,我们发现即使所需答案是固定的,在推理过程中引入多样性也可以极大地受益; 因此,我们利用采样来实现这个目标,采样通常用于开放式文本生成(Radford等人,2019;Brown等人,2020;Thoppilan等人, 2022)。需要注意的是自一致性只能应用于最终答案来自固定答案集合的问题上,在原则上如果可以定义多个生成之间一致性良好度量值(例如两个回答是否相同或相互矛盾),则该方法可扩展到开放式文本生成问题上。
EXPERIMENTS
We conducted a series of experiments to compare the proposed self-consistency method with existing approaches on a range of reasoning benchmarks. We find that self-consistency robustly improves reasoning accuracy for every language model considered, spanning a wide range of model scales.
我们进行了一系列实验,比较了所提出的自一致性方法与现有方法在各种推理基准上的表现。我们发现,自一致性方法能够稳健地提高每个语言模型的推理准确性,涵盖了广泛的模型规模范围。