
思路
动态规划:
根据跟定条件可以看出,这道题其实就是一个m*n的二维表格。对于给定的位置p(x,y),能到达p的所有可能情况有
- 从上往下p1(x - 1, y) -> p
- 从左往右p2(x, y -1) -> p
那么达到p的所有可能路径是paths(p1) + paths(p2);
在这个二维表格中,从初始位置到边界的任何位置,都只有一条路径。所以每个边界上的位置的所有可能路径都是1。
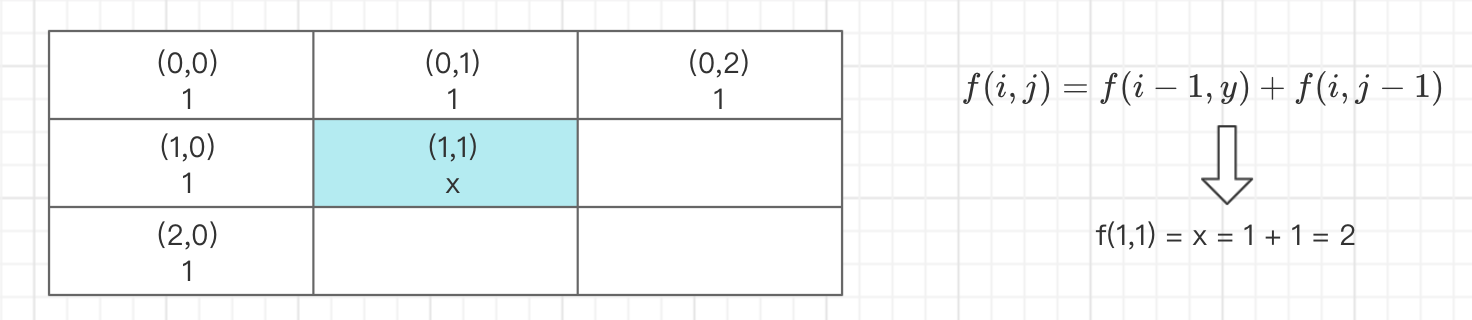
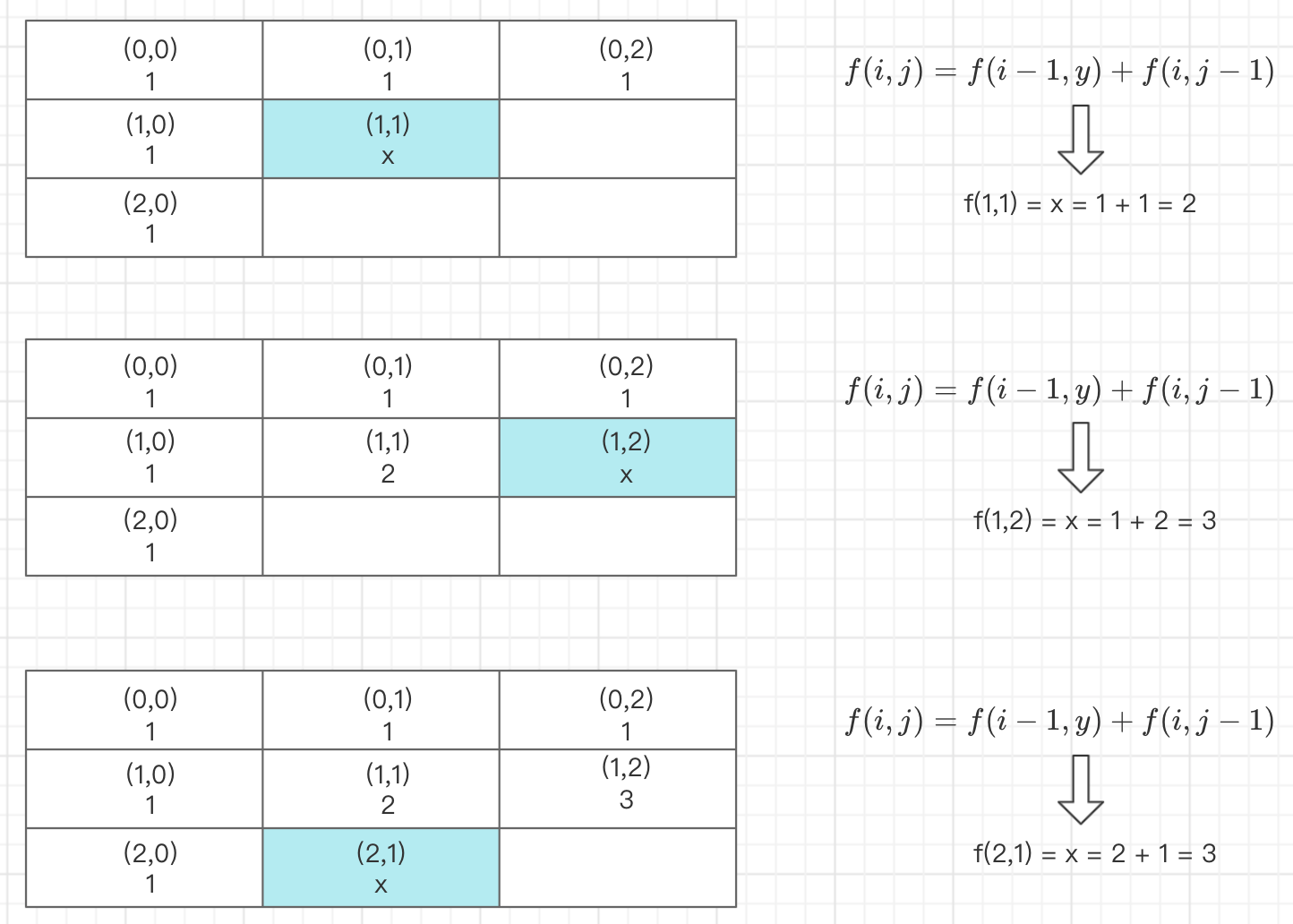
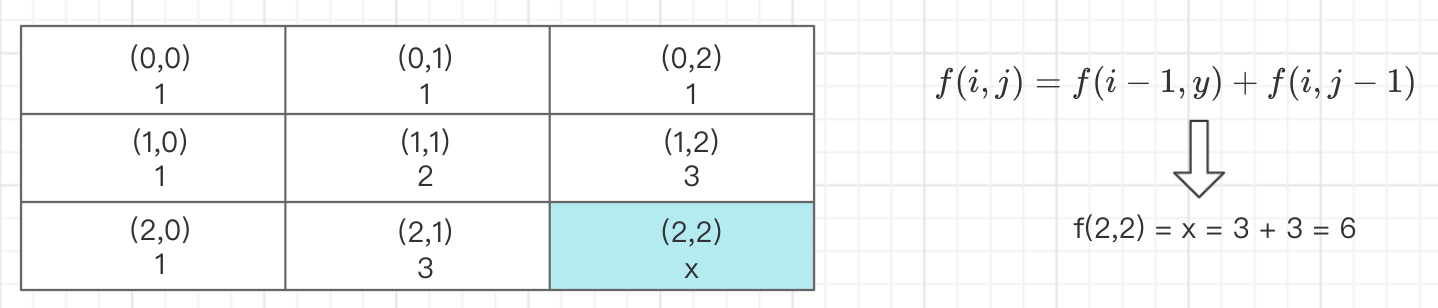
所以如上图所示,对于给定表格的任何位置,所有路径可能的动态转移方程为:

由上图可知,机器人到达(1,1)位置的所有可能路径为:1+1=2;
到达(1,2)位置的所有可能路径为:2+1=3;
以此类推:达到最右下角(2,2)的所有路径可能为3+3=6.
实现:
public int solution(int m, int n) {
int[][] dp = new int[m][n];
for(int i = 0; i < m; i++) {
dp[i][0] = 1;
}
for(int i = 0; i < n; i++) {
dp[0][i] = 1;
}
for(int i = 1; i < m; i++) {
for(int j = 1; j < n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}
|
效率:
时间复杂度:O(m n)
空间复杂度,使用了mn的空间用来存储结果集,所以空间复杂度也为:O(m * n)。
递归:
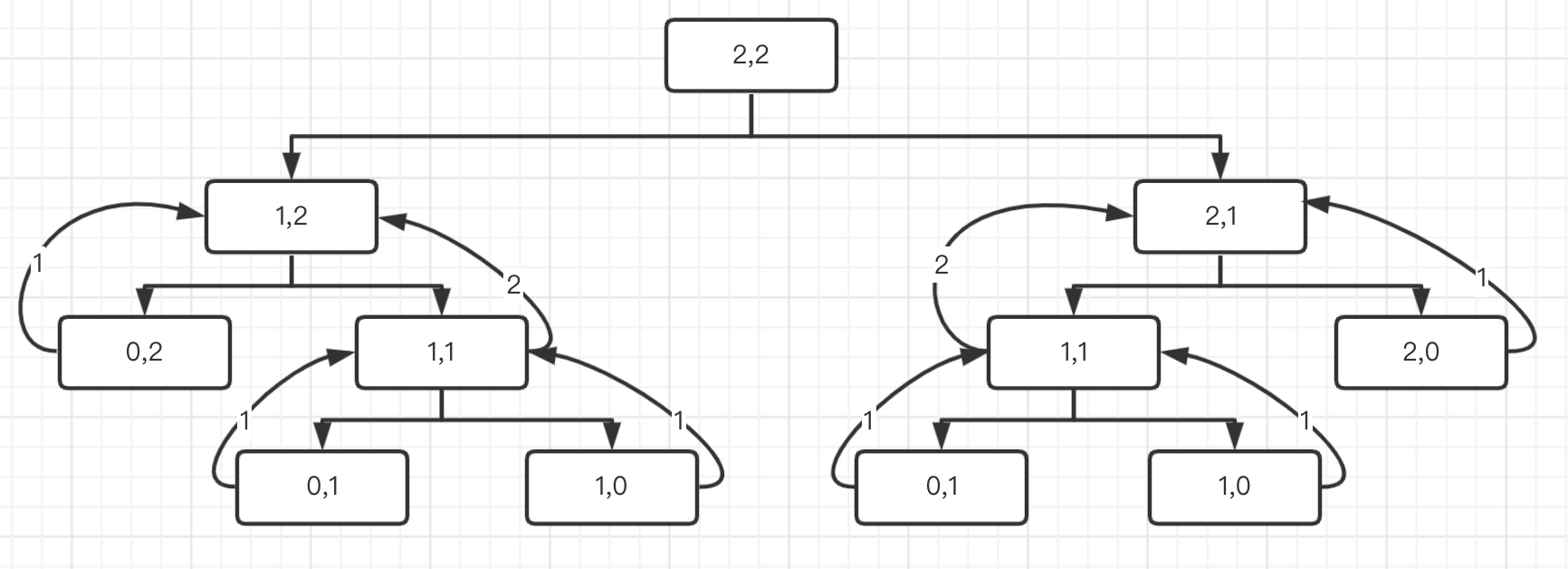
由上面动态规划可知,要计算表格某个位置的所有路径,只需要知道他上面位置和左边位置的所有路径,并求和即可。
那么对于3*3的表格,计算机器到达(2,2)位置的递归过程为:
实现:
public int solution(int m, int n) {
return caculatePaths(m - 1, n - 1);
}
private int caculatePaths(int targetX, int targetY) {
if(targetX == 0 || targetY == 0){
return 1;
}
return caculatePaths(targetX - 1, targetY) + caculatePaths(targetX, targetY - 1);
}
|
递归改进:
上面递归算法因为存在大量的重复运算,导致算法耗时比较大。下面通过新增数据字典,将计算过的结果缓存起来。这样就大幅度的降低计算耗时。
实现:
public int solution(int m, int n) {
int[][] dic = new int[m][n];
return caculatePaths(m - 1, n - 1, dic);
}
private int caculatePaths(int targetX, int targetY, int[][] dic) {
if(targetX == 0 || targetY == 0){
return 1;
}
int upPos = dic[i - 1][j];
if(upPos == 0) {
dic[i - 1][j] = caculatePaths(targetX - 1, targetY);
}
int leftPos = dic[i][j - 1];
if(leftPos == 0) {
dic[i][j - 1] = caculatePaths(targetX, targetY - 1);
}
return upPos + leftPos;
}
|





